Substring Matching over Field-Level Encrypted Data

Data security is our priority, and we aim to defeat data theft by offering user-friendly solutions for engineers. Our technology allows for the secure storage and search of sensitive customer data, providing a viable alternative to SQL databases.
To achieve maximum security, data encryption is performed by the application during runtime. Our primary technological challenge is to enable search functionality on encrypted data, without compromising its security. It's important to note that our focus is solely on search capabilities, not on performing calculations on the encrypted data.

Searchable encryption definition

This article will use the term "searchable encryption" to describe the ability to perform substring matching on data that is supposedly encrypted. To be precise, the data is first indexed and then encrypted. And when searching over it, we will be using this index. So a search is really going over the index data and finding the relevant strings, according to a pattern matching as well.

The weakness of data encryption at rest for cloud apps

Encryption of data at rest is commonly used and enabled by default, but it is a weak form of data protection in the cloud era. This is because it is unlikely that someone will steal a hard drive from a data center, and if you have the credentials to the database, it will automatically decrypt the data and serve it in plaintext, making it transparent for everybody.

Application-level encryption is safer

Application-level encryption solves this by protecting the lower layers from data theft by encrypting plaintext data at the field or column level, making it unreadable to those who gain direct access to the database. The encryption keys, accessible to the application only, eliminate data exposure risk at both the database and file system levels.

Encrypting fields in a database breaks functionality

Encrypting data at the application or field level can create challenges for working with the data seamlessly.  One of the main issues when the data is encrypted, is that it can no longer be queried directly. A simple query to select a phone number from a client table based on an email address would fail because the email column contains encrypted data.  This is because the query would attempt to compare a plaintext email address to an encrypted email address, which would not match.

Think how the following SQL line breaks:

SELECT phone_number FROM clients WHERE email = $1

Approach #1: Deterministic encryption is seamless but limited

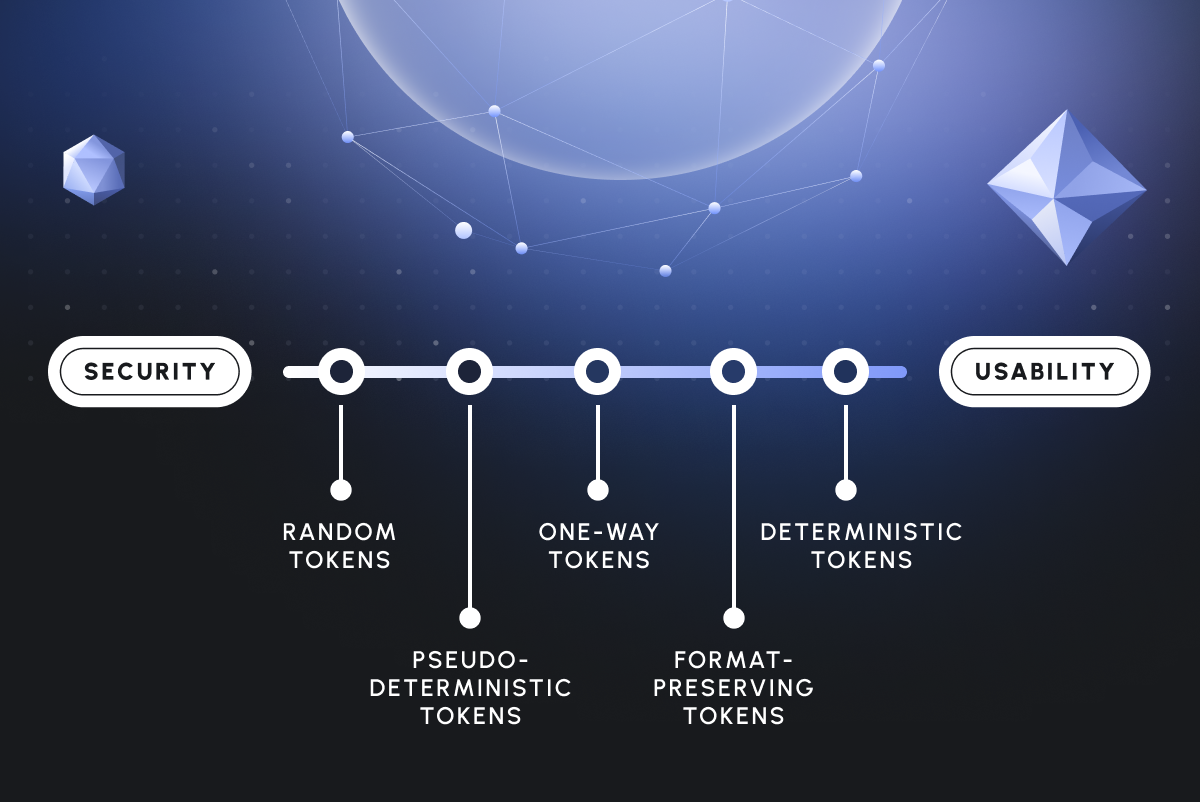
One way to achieve this is through a deterministic encryption scheme, where every input is mapped to the same encrypted ciphertext. This can be done in AES by deterministically calculating the IV, and encryption libraries like Google Tink also offer this functionality.
The deterministic property is very useful for searching data, as in an exact match fashion, hence it’s limited. Existing queries remain the same, but the arguments are encrypted before querying. For instance, if a plaintext email address is stored encrypted with the deterministic scheme, the same cipher will always be generated for that email address. When we want to look up an input, we can encrypt it with the same deterministic method, and comparing them will yield the correct results. This allows a database that is oblivious to the underlying ciphertext to continue to perform well.
Important security consideration: Deterministic encryption inadvertently reveals some information about the plaintext, as identical values consistently generate the same ciphertext. While data encryption is employed, indexes typically remain unencrypted. We find weakness problematic and therefore it will be addressed later on.

Approach #2: Non-deterministic encryption with a deterministic blind index

To upgrade the first approach, we can use blind indexes as they provide a safer alternative, because we can salt them. Blind indexes are deterministic, one-way integers (or sets of bytes, really) derived from the original data and stored along the encrypted ciphertext. Hashes, HMACs, or PRFs (pseudorandom functions) can all serve as blind indexes. To search data using a blind index, the blind index value of the input string is calculated first. Then, the blind index column is queried, and the result matching columns are decrypted in memory.
From deterministically encrypted data that might potentially reveal some information about the underlying plaintext, we move to non-deterministic encrypted data. By using a deterministic blind index, that can be easily salted, which enables easy querying for exact matches using only integer comparisons. Although this approach requires an additional column in the table.
It's important to note that the integer size of the blind index impacts collision probability. To minimize the chance of collisions and inaccurate results, a 128-bit size is recommended, although it may affect storage space and lack native database support. Generally, the smaller the integer, the greater the likelihood of collisions.

Let’s quickly see how it’s done when inserting a new plaintext data encrypted:

1. Calculate HMAC on the plaintext input -> blind-index
2. Encrypt the plaintext input -> ciphertext
3. Insert both ciphertext and blindindex to the database

When looking up a record by an encrypted field:

1. Calculate HMAC on the plaintext input -> blind-index
2. Look up the record
   SELECT phone_number FROM clients WHERE email_blindindex = $1
3. Decrypt the encrypted data fetched from the database

AWS has recently incorporated searchable encryption functionality through the use of 'beacons,' which are essentially blind indexes implemented using a truncated HMAC. Thus, not supporting substring matching over the encrypted data, touché.

pgcrypto to the rescue?

To encrypt sensitive data within a database, developers frequently utilize extensions or libraries like pgcrypto. These tools provide a suite of cryptographic functions that can be seamlessly integrated into database queries and operations. By leveraging pgcrypto or similar solutions, developers can apply encryption algorithms directly to data stored in database tables, ensuring that confidential information remains protected even if unauthorized access to the database occurs.

Pgcrypto is excellent for securely storing data and passwords within a database, but it has several shortcomings that make it unsuitable for our purposes:

1. It requires you to do key management on your own. Unfortunately today, it’s done in a lousy way where there’s one key and it’s exposed everywhere throughout the architecture.
2. Encryption/decryption occurs within the database, requiring the transmission of plaintext data to the database, which we consider untrustworthy.
3. Log files may contain sensitive data due to the database handling plaintext data.
4. Securely searching data necessitates decrypting all rows sequentially in memory, resulting in extremely slow performance (whole seconds for millions of rows).
5. While fast searchability can be achieved through trigram indexing, the indexing data is stored in plaintext.
   This is unacceptable, after all, what’s the point of encrypting the data.
6. It lacks native support for substring matching.

Due to these limitations, we had to develop our own searchable encryption solution.

The limitation of the simple blind indexing approach

While the previously mentioned approaches are valid and documented, they only support exact-match searches. The blind index calculation is based on the entire input, offering no flexibility for partial matches. This limitation prevents searches for values with specific prefixes (e.g., "Jo*") or suffixes (e.g., "*@company.com").
Substring matching, especially within encrypted data, presents additional challenges. Matching the beginning, ending, middle, or a combination of these within a textual value becomes increasingly difficult.
To expand our product's capabilities, we've implemented substring and glob-pattern matching over encrypted data.
This blog post will detail our research journey towards achieving a high-performance implementation.
Another fun blog post provides a deep dive into database cryptography, exploring the complexities and constraints of searchable encryption. It also discusses the drawbacks of deterministic encryption and other pertinent subjects.

Piiano Vault

Piiano's primary product, Vault, is a secure database that safeguards sensitive data, including Personally Identifiable Information (PII), Payment Information (PCI DSS), Protected Health Information (PHI), and confidential secrets like customer webhook tokens. Vault encrypts this information and utilizes Postgres as its underlying storage system.
We recently added full support for secure, seamless and performant substring matching over field-level encrypted columns.
In our implementation we have some further requirements:

• Full security for both indexing data and encrypted data
• No full plaintext data tables in memory
• High performance
• Database agnostic
• Support for horizontal scaling

Our performance goals

The goal is to support substring matching queries with the following requirements:

• A database with a few millions of rows (records)
• Five encrypted VARCHAR properties, each with a length of 20 characters
• Query response time of up to 20 milliseconds
• Paginated API calls returning up to 100 results each

As a performance benchmark, note that substring matching using the LIKE operator in a standard PostgreSQL database typically returns results in a few to tens of milliseconds, depending on the specific glob pattern used. For reference see this and this benchmarks over one million strings.
A couple of notes for the sake of accuracy:

1. We do not actually search over the encrypted data itself (as shown in approach #1). Instead, we perform lookups on indexes.
2. Searching encrypted data involves securely indexing the data and subsequently utilizing that index to retrieve the encrypted data. That’s the whole game now.

Buckle on.

Approaches towards efficient and secure substring matching

The naive way - Decrypting everything in memory

Fetching and decrypting all the encrypted data in memory to search over it is a possibility. However, for a million rows, this could mean fetching up to approximately 20MB of data per query. This method would be slow and expose all the encrypted data in memory.
While keeping all the data in memory, using something like Redis is an option, it goes against product requirements. Given large amounts of data and small servers, this solution could be problematic. Additionally, this would not address potential security issues like compromising machine RAM.

A word on homomorphic encryption

Homomorphic encryption is excellent for data sharing and zero-knowledge environments, but it is not a requirement for us. Additionally, it is currently too slow for practical use in transactional systems.
Ultimately, organizations like banks and governments will always need to store personal and sensitive information.
Therefore, we find it irrelevant and we assume that you also need to store and work with user data seamlessly and securely to prevent data breaches.

On indexing, coverage and limitations

A single blind index covers the full length of the search input. This may have some potential information leakage, but the biggest downside is that it only supports a match of everything or nothing, and is therefore not suitable for our substring matching goal.

Working with multiple blind-indexes

Let's assume we divide our search input into several parts. This allows us to find a good balance between coverage and the number of indexes needed. As a result, we won't need many indexes and it can still be high-performing. For instance, if an application always searches by the first 3 letters of the input, we could create a blind index solely for that part. This effectively enables search for any string by its first three letters.

Now let’s expand this by creating multiple blind indexes for the same search input. This time, we index the first 3 letters and the next 3 letters of the search input, which results in a more complex implementation and yet more flexible search capability. Now imagine we can decide on how we divide the input string and by what lengths to get a fully flexible search.

Although this approach is feasible, storing numerous blind indexes can be storage-intensive. And who decided we need to break everything into 3 characters or technically trigrams? This raises the question of how much overhead we are willing to allocate for a single column. We will later see why trigrams are a good fit here, for now let’s assume that’s what we are going to use.

A single blind-index column containing a million rows of 128 bits requires more than 120 MB of storage (128 * 10**6 = 122 MB). This storage requirement can increase linearly for each indexed 3-character segment, becoming quite substantial for long strings. Even when using custom-defined VARCHARS of 20 characters, the storage needed would be approximately 840 MB (20 / 3 * 120). In comparison, the internal index size for the same data (1 million records of VARCHAR 20) within PostgreSQL is only around 40 MB.

Now imagine, how many such indexes would we need to store to support any substring matching of the search input?

The Bloom Filter data structure is known for its space efficiency when storing numerous values at once. Could this data structure be adapted to store sufficient information to allow substring matching?

Bloom filter

There are many excellent resources for learning about Bloom filters in depth (see https://brilliant.org/wiki/bloom-filter/ and https://samwho.dev/bloom-filters/).

In brief, a Bloom filter is a space-efficient, probabilistic data structure based on hashing. 

💡Consider it as a collection where you can add elements and check if they exist. If the filter indicates that an element is not in the collection, it's definitely absent. Conversely, if the filter indicates that an element is present in the collection, it's only potentially there.

The filter, which is a bit array of fixed size, works by setting specific bits to 1 when data is added. Querying the filter involves checking if the corresponding bits are set to 1. This process may result in some false positives, which, as we will see later, can enhance security against information leaks of the underlying plaintext.

💡Practically we need a filter long enough to avoid excessive noise and collisions (more on that later).

A Bloom example

Let's consider an example: suppose we have a filter represented by 10101101 (corresponding to indexes 0, 2, 4, 5, and 7). Yes, along this blog, we’re showing positions from left to right, go mathematicians.

To determine if this filter includes a particular search input, we first calculate the filter for that input, which we will call a “mask”.

If the mask is for example 00100001 (indexes 2 and 7), and as we can see those indexes are present in the original filter, the input is possibly included.

However, if the input was mapped to 00000011 (indexes 6 and 7), since index 6 is not in the original filter, we can conclude that the input is definitely not included.

Here is a sample code to calculate the Bloom filter in Go (our language of choice for the vault at Piiano), without any external library:

1const (
2   bitLen       = 128
3   ElemSizeBits = 64
4   hashCount    = 5 // k=5
5   elemSizeBytes = elemSizeBits / 8
6)
7
8
9type Filter [bitLen / elemSizeBits]uint64
10
11
12func CreateFilter(in string) Filter {
13   var bloomFilter Filter
14  
15   hash := sha256.Sum256([]byte(in))
16   for i := 0; i < hashCount; i++ {
17       // Assuming 128bit filter.
18       index := uint64(hash[i]) % bitLen // Currently using 128 bits, so 1 byte per hash is enough.
19       bytePos := index / elemSizeBits
20       bitPos := index % elemSizeBits
21       bloomFilter[bytePos] |= 1 << bitPos
22   }
23  
24   return bloomFilter
25}

This code assumes a Bloom filter index size of 128 bits, represented as an array of [2]uint64, as Go is limited to 64 bits integers max. To set the filter's bits, we calculate a hashCount number of different random numbers as indices and then take a modulus to fit the size of the filter. This process is repeated for each input that needs to be indexed by the filter, with additional bits being set for each new input.

Two important things to note:

1. hashCount is set to 5 which is the best ratio we found for having a few millions of records indexed well, more on false positives below.
2. different random numbers - In Bloom filter, it’s all about hashing and uniformity, we use SHA, but you can come up with many other methods. Bloom requires calculating different hashes for the same input. But to save running time we use a single SHA, as it’s long enough, and break it down to multiple parts, and then it’s good enough for our case. Just an optimization.

But how can Bloom filters include information about whether a string contains a certain substring?

Trigrams

That's where trigrams come into play. A trigram is a sequence of three letters (an N-gram is a sequence of N letters) from a string.

For example, the string "ABCDE" can be split into three trigrams: ABC, BCD, and CDE. Adding these trigrams to a Bloom filter creates a structure that can answer whether a trigram is included in a string, in one shot, without actually storing the substring itself.

Is ABC anywhere in the string (which means it’s a substring)? If the Bloom filter says yes, then it's probably there. Is XYZ in the string? If the Bloom filter says no, then it's definitely not.

Is ABCD in the string? Well, ABCD consists of ABC and BCD, so both need to be queried. If the Bloom filter indicates both are present, then ABCD is probably a substring of the original string.

💡The beauty and advantage of using Bloom filters is that it indexes data in a position independent way, and it requires a simple bitwise and operator to check membership. You just do a single look up and you know whether a string contains a trigram or not, without the need to scan the string at all (byte by byte, etc), just querying the Bloom filter once. Technically doing simple mask operations which are super fast. This is great for performance and to know that possibly the trigram appears in the string and we should examine it further (for verification and finding its position).

💡Note that for a search to work using Bloom filters, it must match all trigrams!

Here is a Go function to return all the trigrams of a string:

1// generateTrigrams generates all trigrams of the given input text.
2// Note: Assuming the input is of length 3 or more.
3func generateTrigrams(text string) []string {
4   var trigrams []string
5   for i := 0; i < len(text)-2; i++ {
6       trigrams = append(trigrams, text[i:i+3])
7   }
8   return trigrams
9}

Why Blooms and trigrams are so great

💡The high performance of searchability with this mix is mainly due to the following reasons:

• Granularity of Triplets: Triplets are granular enough to find a sufficiently unique 'piece of information' which reduces the possibility of false positives.
• Position Independence of Bloom Filter: The Bloom filter's position independence means that the position of a trigram within the string doesn't matter. Which means that trigrams can be looked up in O(1) time.
• Bloom Filter Calculation: Calculating a Bloom filter is fast and easy despite requiring some hashing.
• Noise Insertion: It intentionally introduces noise, which enhances security.

This approach gives us flexibility in balancing overall performance. We have control over the noise ratio, which we'll detail in the upcoming section. We can also adjust the length of the information pieces we use; in this scenario, triplets or trigrams work well. Consider the alternative of single-byte indexing: for each letter, you'd retrieve all candidates containing that letter, resulting in high noise and substantial filtering requirements.  Thus, we also manage the number of collisions.

Indexing in the database or in-memory

Once we got the data encrypted in the database, it was natural and easy to store the indexing data (the Bloom filters) next to it, also in the database. However, doing so we encountered severe performance issues when running queries.

The biggest challenge we faced while implementing this feature was utilizing the database's native indexing capabilities on our own indexing data to enable very fast searches.

Indexing such data in the database was not possible due to numerous constraints we encountered, although we explored many different techniques, but everything produced poor results.

The advantage of a Vault is that we can securely execute our proprietary code and indexing algorithms within our protected and segregated environment, outside of the database. While we won't delve into the specifics of our indexing process, we will mention that it occurs in-memory within the Vault server. Below, we address how we ensure the secure storage of the indexing data in the database.

False positive rate

Last step before we can get into implementation - the Bloom filter needs to be tuned to be optimal for our use case. We can use the Bloom Filter calculator to help us decide on the size of the filter, or the false-positives rate, as well as the rest of the parameters.

With our described goals, the encrypted properties will be a maximum of 20 characters, which means up to 18 trigrams. A 128-bit filter appears to be a good compromise for storage and memory size. 128 bits x 1 million records x 5 properties is approximately 600MB, which will not be an excessive load for modern databases or application memory.

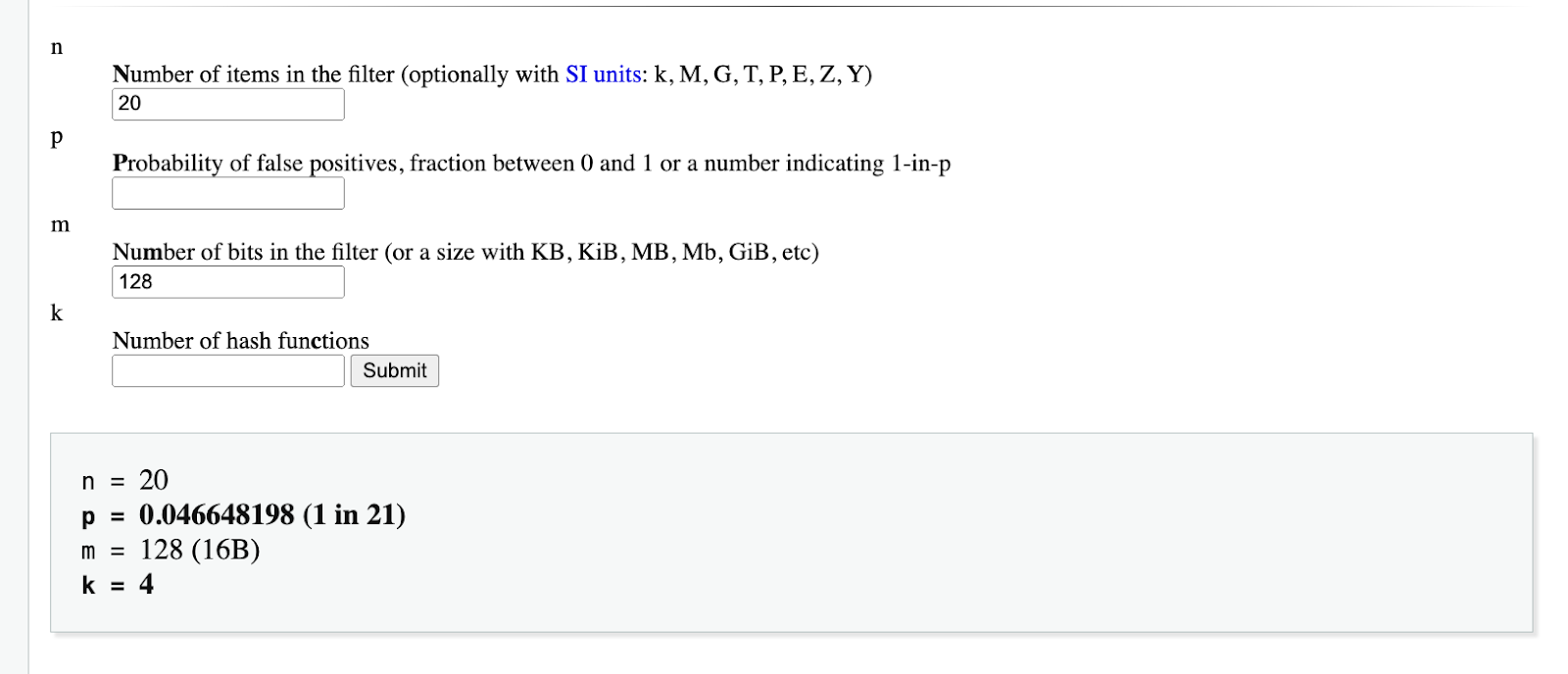
The probability of a false positive for a single trigram is 1 in 21, based on this calculation. Since each element of the filter is independent, the probability of N trigrams resulting in a false positive is 1 21n for substring queries that consist of more than one trigram (which is any substring with more than 3 characters). The false-positive rate improves exponentially; for example, with just two trigrams (a minimum of 4-letter substring), the false-positive rate is 1/441.

Eliminating false-positive candidates

The in-memory index also allows us to more effectively handle false positives generated by Bloom filters and trigrams. For example, ABCD will match the string ABCDE and also ABCXXXBCD because both ABC And BCD are there. These false positives can simply be filtered out after the query is done.

Our indexing table holds corresponding UIDs to the rows inside the database for further fetching the actual encrypted string data, because it’s not in the memory. In the database it would look like:

uid                | name
-------------------+--------------------------------------------------------------------------------------
376112274113396736 | AfcIp1B+kFBh1DW+/OGJjnjJR/LHqwRkN2QnKZWfpEIft+QXXIMT8Mm1RqrM56kgTb+x2E3K+Yiz9XTguyjU
376112274125979648 | AfcIp1BdXDezFXFYOmNd6LcXpT7fRe3NOpSpXPbgbxp+kcoZPDm+mbEku40ev7pHG+Y+k+1jZUxKtTZFgMvv
376112274134368256 | AfcIp1DtrgwAoq6hMWiOVt7qagfbz+Z+DuodkuRUA5HKKyObHQrc5l0nNTC0Spz1Jlp80UgMxSjq9pgYGgzL
376112274142756864 | AfcIp1Ae4+wZ7CiFv5H4r3UTQUxgQMAUDZgbyFgIz6ZbZqR136UXuCkNoRiLV9UrO62RXfrj3dy5MmS96rVZ
376112274159534080 | AfcIp1D+XgtnUVE5WP1Oyp/R5/HV+op0o7uzbITiBZxNwdMjCxSEwJYpuido59urd5UHYosBqKmT0a9n8CLU

In practice, when the application receives a substring query (e.g., ABCD), it can be used to query the index and retrieve the UIDs of potential matches. After these UIDs are pulled from the database, the additional encrypted columns are decrypted. Since some of these may be false positives, each result can be checked individually against the input query string, and only the actual matches are returned.

The full algorithm in high level

Now that we understand Bloom filters, trigrams, and the probability of false positives, let's explore how these elements combine to form a functional substring searching algorithm.

String Insertion

Step 1:
‍Index a string by breaking it to trigrams. Hash each of them and insert it into a Bloom filter index.

Step 2:
Insert the result together with the encrypted field to the database.

String Searching

Step 1:‍
Same as before, calculate the Bloom filter index (mask) for the string to look up for.

Step 2:‍
Scan the index table in memory and prepare a list of all UIDs of candidate rows in the database - the ones with the right mask.

💡Step 3:
And this is the interesting part. To cope with the false positives -
Read all stored and encrypted strings by their UIDs from the database. They potentially contain the substring we’re searching for.

Step 4:‍
Decrypt them in memory. And iterate through them all.
Do real in-memory substring matching to validate that they really contain the required substring. Discard the ones mismatched (ones that got back because of the false positives issue) and build a list of the ones that have a match for real.

Step 5:
Return the matching list, in a paginated manner.

[Bonus] Step 6:‍
Vault is a multi-instance cluster and thus requires a cache for synchronization for faster performance. This eventually consistent cache has configurable read/flush intervals.

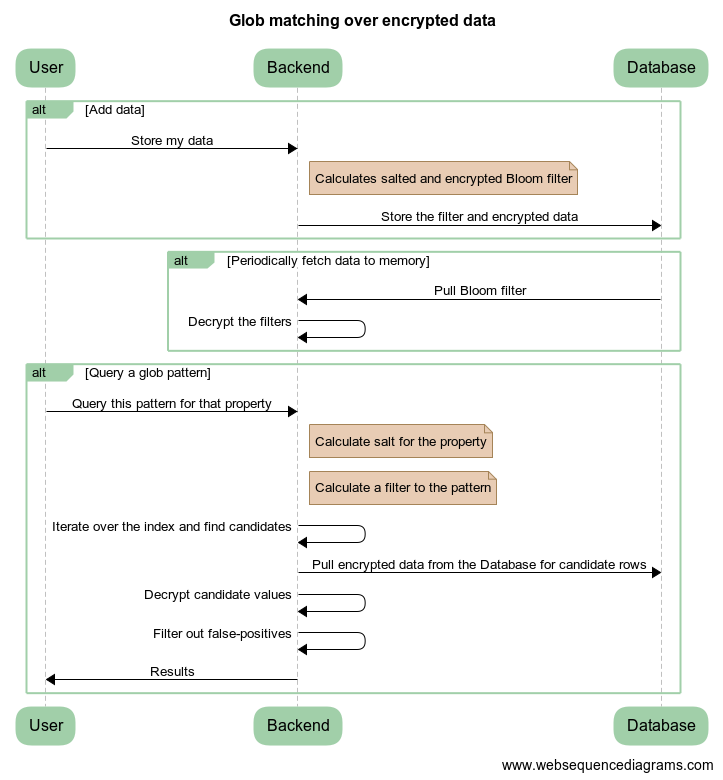
Flow Graph

In the following diagram you can learn that the Bloom filter indexes are encrypted too in our implementation, which is awesome. If an attacker compromises the database directly, they still can’t make anything of the plaintext data out of the indexing information. Note how we fetch the actual encrypted columns once we know which ones we need to fetch.

More than substring matching

Given the indexes are in memory, a more sophisticated query pattern called Glob pattern, can be leveraged.

We could take a glob pattern, say *ABCD* , extract the trigrams out of it and query the filter. Then, apply the glob over each of the results and return only those that match. This allows a much more flexible query patterns:

• Substring matching: *John* - All the users that have “John” in their name.
• Prefix matching: John* - All the users whose names start with “John”.
• Suffix matching: *Copperfield - All the users that their name ends with “Copperfield”.
• Complex queries: Dr. * Doe - All the doctors with the last name Doe.
• And even more granular queries if your heart desires: ?ing - All the 4 letter names that end with “ing” - Ming , Ning.

💡Support for globbing introduces another layer of false-positives though. For example, take the following query: John* which clearly says “find all the names that start with “John”. We split to trigrams: Joh, ohn and query the index - and unfortunately the name David Johnson matches too. Well of course it does - both the trigrams appear in it. If you remember the trait of Bloom filters is that they index stuff in a position independent way, but we want only names that start with it. There are ways to optimize this even before it gets to the filtering in memory, but we won’t get into that here, although we implemented it for maximizing performance for our solution.

Open source glob library

In terms of implementation - most glob pattern libraries are focused on file path searching or for URL matching, and as such are tied directly to the separator character / (on unix based systems, \\ for windows). The libraries that don't treat the separator character differently, are either unmaintained for years now, they don’t implement ? matching or supporting escaping.

As such, we decided to open source our glob matching logic in a Go library. This package supports both * and ? matching, as well as escaping them, and other utilities that are helpful for Bloom filter indexing like returning the literals of the pattern itself.

Preventing data exposure and info leaking of the indexes

Data encryption is primarily used to prevent information disclosure during a breach. However, storing additional indexing data alongside the encrypted data could inadvertently reveal information about the underlying encrypted content.

For example, if a hash is stored as a blind index next to encrypted data for a column called first_name, and this data is breached, could we learn anything about the plaintext from it? Other than the fact that two identical hashes necessarily mean the same underlying value, using statistics, we can assume that the most commonly found hash is likely to be the most common name, if the number of samples is large enough.

Similarly, with the Bloom filter for trigrams, the most commonly found bits may correspond to the most commonly used trigram, which are 3-letter combinations. How can this be avoided?

Salting the indexes

By adding a unique salt per column and per deployment to the Bloom-filter hashes, we can prevent matches between data across different columns of the application and also between different deployments of the application. As a result, inserting the same string into different columns would produce a different Bloom filter due to the salt.

Encryption of the indexes

However, salt alone is insufficient. Identical values within the same column would still utilize the same hash, allowing for statistical analysis to be applied to that column independently.

One might wonder how this differs from simply decrypting and using the values themselves. Here are key advantages:

• Security: Sensitive information is not entirely exposed in memory.
• Space: The index is smaller than the data, reducing memory requirements for the application and database load.
• Performance: Querying the index table is fast, often requiring only simple bitwise AND operations.

Given that we want to encrypt the index, the question is which cipher to use considering the millions of records (and indexes) that need decryption. While strong ciphers like AES GCM work, they are slower and don't allow entry-level operation, as we want to maintain random access to the index.

We propose AES ECB with a different key per field. While less secure, as two filters may still appear similar, bit-level statistical attacks are no longer viable. This solution is the most cost-effective in terms of speed and storage, allowing us to work at the entry level and not the full block of the index section.

Normally, using ECB is discouraged due to its inherent weakness. However, in our case, it's sufficient to protect the short filters (128 bits). While ECB does not provide semantic security, this risk is acceptable within our threat model.

Index scanning performance in lab

The performance breakdown from our logs, of the average query for a page of 100 results with a search pattern over a million records on a macbook pro M1 chip:

• Creating the filter to query - Immediate
• Query of the index: ~2-5ms, our internal logs show:
  • "message": "Substring index query for property name took 5.2585ms. Found 8934 candidates"
• Database querying to fetch candidates: ~20ms
  • "message": "DB query took 15.186875ms on iteration 0. Found 400 candidates, after filter left 318"

Actual production deployments that leverage managed instances and databases will improve the performance substantially.

Piiano Vault SaaS performance

Piiano Vault SaaS provides end-to-end performance of 10-20ms or less for substring matching search requests over millions of records. Timing is measured when the API request is received and ends as soon as it returns, excluding any network roundtrip time.